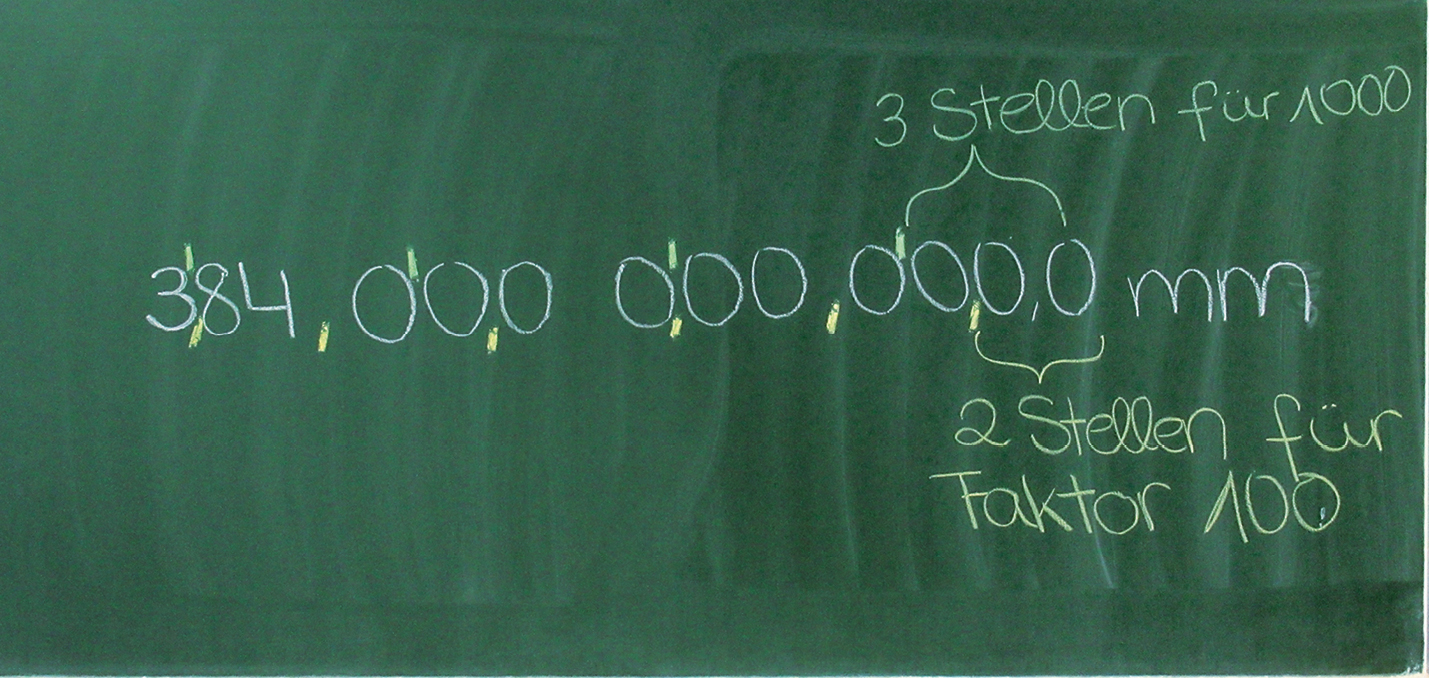Stell dir vor, du hast ein ganz normales Blatt Papier. Und jetzt stell dir vor, du könntest dieses Blatt immer und immer wieder falten. Was, wenn du es so oft falten könntest, bis es bis zum Mond reicht? Klingt verrückt, oder? Aber genau diese Frage – wie oft man ein Blatt falten muss, um zum Mond zu kommen – wollen wir heute gemeinsam untersuchen. Wir richten uns an alle Schülerinnen und Schüler, die Spaß an Mathe, Wissenschaft und verrückten Gedankenspielen haben!
Die magische Macht des Faltens: Ein exponentielles Abenteuer
Warum ist das so eine spannende Frage? Weil sie uns ein wichtiges mathematisches Prinzip vor Augen führt: die exponentielle Zunahme. Exponentiell bedeutet, dass etwas nicht linear, also gleichmäßig, wächst, sondern immer schneller. Stell dir vor, du legst jeden Tag das Doppelte von dem Geld, das du am Vortag hattest, in deine Spardose. Am Anfang ist es nicht viel, aber nach ein paar Tagen hast du plötzlich eine riesige Summe!
Das Falten eines Blattes Papier funktioniert ähnlich. Jedes Mal, wenn du es faltest, verdoppelst du die Dicke des Papiers. Das klingt harmlos, aber die Dicke nimmt rasend schnell zu.
Was ist eigentlich die Dicke eines Blattes Papier? Ein normales Blatt Papier ist ungefähr 0,1 Millimeter dick. Das ist sehr dünn, kaum vorstellbar! Aber diese winzige Dicke ist unser Ausgangspunkt für das große Falt-Experiment.
Die ersten Faltungen: Von Millimetern zu Zentimetern
Lass uns die ersten Faltungen mal Schritt für Schritt durchgehen:
- 1 Faltung: 0,1 mm x 2 = 0,2 mm
- 2 Faltungen: 0,2 mm x 2 = 0,4 mm
- 3 Faltungen: 0,4 mm x 2 = 0,8 mm
- 4 Faltungen: 0,8 mm x 2 = 1,6 mm
- 5 Faltungen: 1,6 mm x 2 = 3,2 mm
- 6 Faltungen: 3,2 mm x 2 = 6,4 mm
- 7 Faltungen: 6,4 mm x 2 = 12,8 mm (also fast 1,3 cm!)
Nach nur sieben Faltungen ist das Papier schon fast eineinhalb Zentimeter dick! Du siehst, wie schnell die Dicke zunimmt. Exponentielles Wachstum ist wirklich beeindruckend!
Die Herausforderung: Die Distanz zum Mond
Jetzt wird es richtig spannend: Wir müssen herausfinden, wie dick das gefaltete Papier sein muss, um die Distanz zum Mond zu überwinden.
Wie weit ist der Mond entfernt? Die durchschnittliche Entfernung zwischen der Erde und dem Mond beträgt etwa 384.400 Kilometer. Das ist eine gigantische Zahl!
Um unsere Rechnung zu vereinfachen, wandeln wir die Kilometer in Millimeter um, damit wir mit der Dicke unseres Papiers in Millimetern vergleichen können:
384.400 km = 384.400.000 Meter = 384.400.000.000 Millimeter (384 Billionen 400 Milliarden Millimeter!)
Das bedeutet, dass unser gefaltetes Papier 384.400.000.000 Millimeter dick sein muss, um bis zum Mond zu reichen.
Die Formel zum Erfolg: Exponentielles Rechnen
Wir wissen, dass sich die Dicke des Papiers bei jeder Faltung verdoppelt. Das können wir in einer Formel ausdrücken:
Dicke nach n Faltungen = Ausgangsdicke x 2n
Wobei:
- n = Anzahl der Faltungen
- Ausgangsdicke = 0,1 mm
Wir wollen wissen, wie viele Faltungen (n) wir brauchen, um eine Dicke von 384.400.000.000 mm zu erreichen. Also müssen wir die Formel umstellen:
384.400.000.000 mm = 0,1 mm x 2n
Um n zu berechnen, müssen wir den Logarithmus verwenden. Keine Angst, das ist nicht so kompliziert, wie es klingt! Im Grunde genommen suchen wir die Zahl, mit der wir 2 potenzieren müssen, um 384.400.000.000 / 0,1 = 3.844.000.000.000 zu erhalten.
Mit einem Taschenrechner (oder einer Suchmaschine deiner Wahl) können wir herausfinden, dass:
n = log2(3.844.000.000.000) ≈ 41,8
Das bedeutet, wir müssten das Blatt ungefähr 42 Mal falten, um bis zum Mond zu kommen! Unglaublich, oder?
Das Problem mit der Praxis: Warum es (fast) unmöglich ist
Obwohl die Mathematik uns eine klare Antwort liefert, gibt es ein riesiges Problem: Es ist in der Praxis fast unmöglich, ein Blatt Papier so oft zu falten.
Warum ist das so?
- Die Größe des Papiers: Bei jeder Faltung halbiert sich die Fläche des Papiers, während die Dicke zunimmt. Nach wenigen Faltungen ist das Papier so klein, dass es kaum noch zu greifen ist.
- Die benötigte Kraft: Je dicker das Papier wird, desto mehr Kraft ist erforderlich, um es zu falten. Irgendwann ist die Kraft, die wir aufbringen können, nicht mehr ausreichend.
- Die Physik des Papiers: Papier besteht aus Fasern. Diese Fasern werden beim Falten gestaucht und gedehnt. Irgendwann sind die Fasern so stark beansprucht, dass das Papier reißt oder sich nicht mehr falten lässt.
Der Weltrekord für das Falten eines Blattes Papier liegt bei 12 Faltungen. Dieser Rekord wurde mit speziellem Papier und viel technischem Know-how erreicht. Es ist also sehr unwahrscheinlich, dass jemals jemand ein normales Blatt Papier 42 Mal falten wird.
Die Mythbusters-Episode: Die Grenzen des Faltens
Die Mythbusters, eine beliebte Wissenschaftssendung, haben sich ebenfalls mit diesem Mythos beschäftigt. Sie haben versucht, ein riesiges Blatt Papier mit der Größe eines Fußballfeldes zu falten. Trotz aller Bemühungen und dem Einsatz von schwerem Gerät konnten sie das Papier nicht mehr als 7 Mal falten. Das hat gezeigt, wie schwierig es ist, die physikalischen Grenzen des Faltens zu überwinden.
Was wir daraus lernen können: Exponentielles Denken im Alltag
Auch wenn wir das Blatt Papier nie bis zum Mond falten werden, ist dieses Gedankenspiel trotzdem sehr wertvoll. Es lehrt uns das Prinzip des exponentiellen Wachstums, das in vielen Bereichen unseres Lebens eine wichtige Rolle spielt.
- Zinseszins: Wenn du Geld anlegst, profitierst du vom Zinseszins. Das bedeutet, dass du nicht nur Zinsen auf dein ursprüngliches Kapital erhältst, sondern auch auf die Zinsen, die du bereits bekommen hast. So wächst dein Vermögen exponentiell.
- Bevölkerungswachstum: Die Weltbevölkerung wächst exponentiell. Das bedeutet, dass die Anzahl der Menschen auf der Erde immer schneller zunimmt.
- Verbreitung von Informationen: Informationen können sich im Internet rasend schnell verbreiten. Ein virales Video oder ein Trend auf Social Media können innerhalb kürzester Zeit Millionen von Menschen erreichen.
- Computerkapazität: Die Leistung von Computern hat sich in den letzten Jahrzehnten exponentiell gesteigert. Das sogenannte "Mooresche Gesetz" besagt, dass sich die Anzahl der Transistoren auf einem Mikrochip etwa alle zwei Jahre verdoppelt.
Wenn wir das Prinzip des exponentiellen Wachstums verstehen, können wir besser einschätzen, wie sich bestimmte Dinge entwickeln und welche Auswirkungen sie haben können. Es hilft uns, die Welt um uns herum besser zu verstehen und fundierte Entscheidungen zu treffen.
Fazit: Die Reise ist das Ziel
Die Frage, wie oft man ein Blatt falten muss, um zum Mond zu kommen, ist vielleicht nicht die wichtigste Frage der Welt. Aber sie ist ein großartiges Beispiel dafür, wie Mathematik uns helfen kann, die Welt zu erkunden und zu verstehen. Wir haben gelernt, was exponentielles Wachstum bedeutet, warum es in der Praxis fast unmöglich ist, ein Blatt Papier so oft zu falten, und wie wir dieses Wissen in unserem Alltag nutzen können.
Denk daran: Auch wenn wir unser Blatt Papier nie bis zum Mond bringen werden, die Reise dorthin – das Nachdenken, Rechnen und Entdecken – ist das eigentliche Ziel. Und wer weiß, vielleicht findest du ja eine Möglichkeit, den Falt-Rekord zu brechen! Bleib neugierig und forsche weiter!