Hey du! Hast du dich jemals gefragt, wie man eine Tangente an einen Kreis konstruiert? Klingt kompliziert, oder? Keine Sorge, ist es gar nicht! Wir machen das heute ganz easy-peasy. Stell dir vor, du bist ein mathematischer Superheld und diese Konstruktion ist deine nächste Mission! 😉
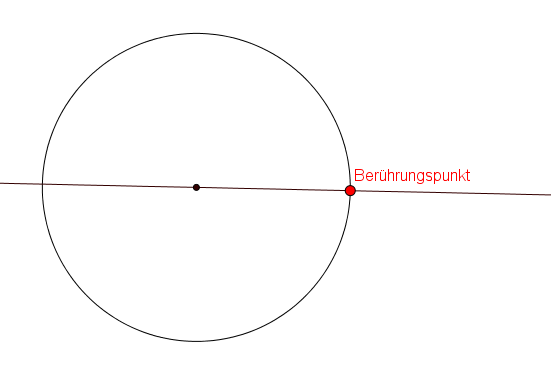
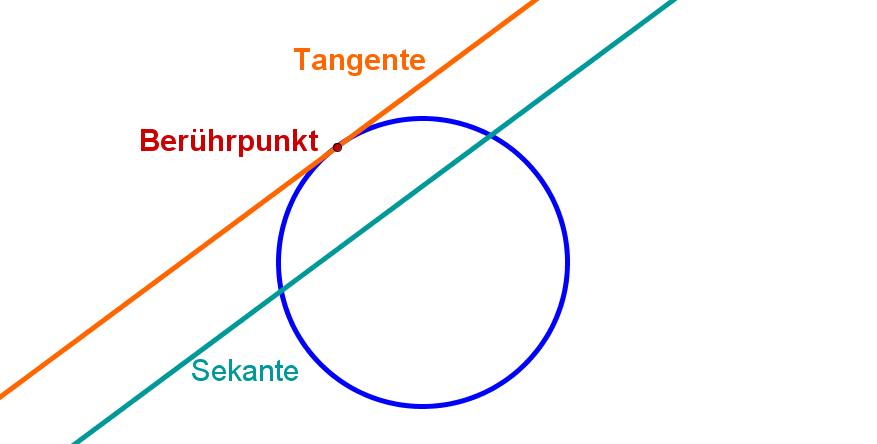
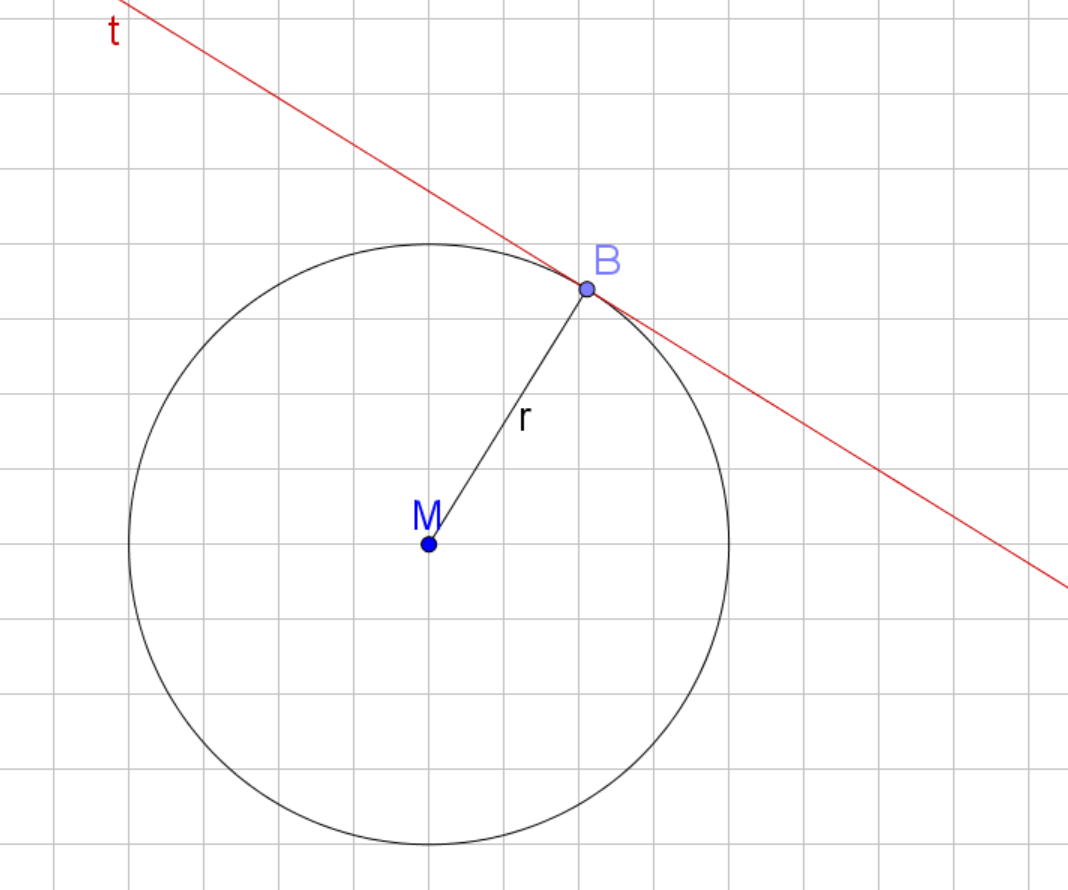
Was ist eigentlich eine Tangente? Denk an einen Radfahrer, der gerade so am Kreis entlangfährt, ihn aber nur an einem winzigen Punkt berührt. Boom! Das ist deine Tangente! Sie berührt den Kreis nur an einem einzigen Punkt, dem sogenannten Berührpunkt, und steht senkrecht zum Radius, der zu diesem Punkt führt. Verstanden? Super!
Die "Ich-finde-den-Mittelpunkt"-Methode
Okay, los geht's! Die erste Methode ist, wenn du den Mittelpunkt des Kreises kennst. Ist das der Fall, bist du schon halb fertig! Wenn nicht… nun, dann musst du ihn zuerst finden. Keine Panik! Das ist auch kein Hexenwerk. Du kannst zwei beliebige Sehnen (Linien innerhalb des Kreises) zeichnen und ihre Mittelsenkrechten konstruieren. Wo sich diese Mittelsenkrechten treffen? Bingo! Da ist dein Mittelpunkt!
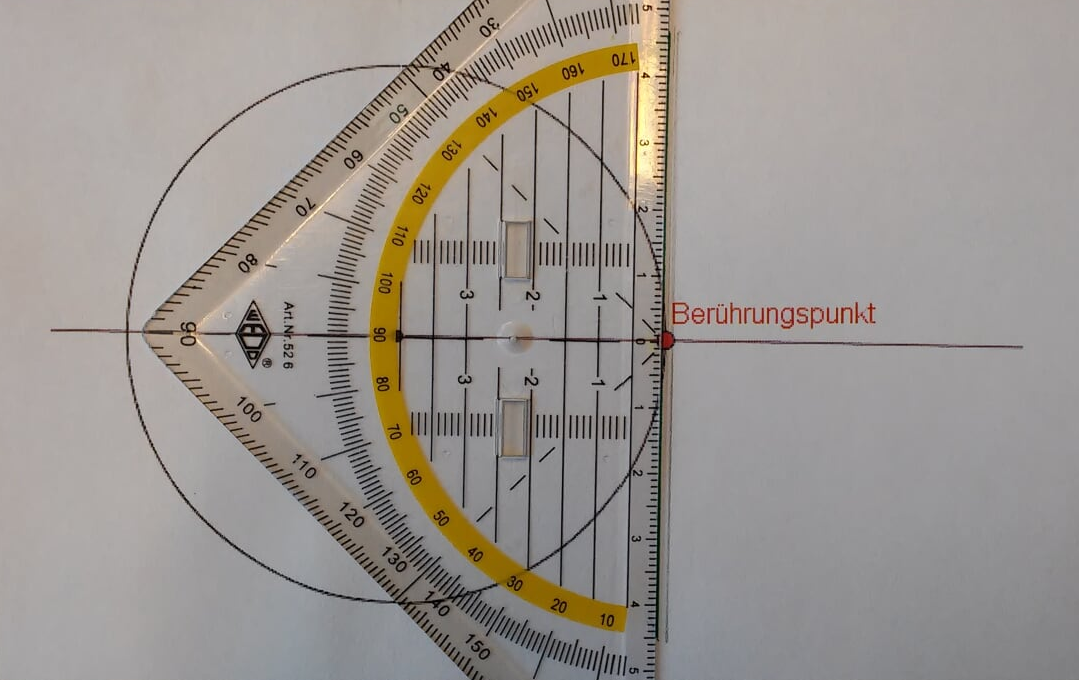
Jetzt, wo du den Mittelpunkt (nennen wir ihn mal M) hast und den Punkt auf dem Kreis, an dem die Tangente berühren soll (nennen wir ihn B, für Berührpunkt, logisch, oder?), zeichnest du einfach eine Linie von M zu B. Das ist dein Radius. 📏
Nun kommt der coole Teil: Du musst eine Senkrechte zu diesem Radius durch den Punkt B konstruieren. Erinnerst du dich noch, wie das geht? Falls nicht, keine Schande! Du kannst einen Zirkel nehmen, ihn auf B setzen und zwei kleine Bögen auf dem Radius zeichnen. Dann verlängerst du den Zirkel, setzt ihn auf die Schnittpunkte der Bögen mit dem Radius und zeichnest von beiden Seiten Bögen, die sich außerhalb des Kreises treffen. Verbinde diesen Schnittpunkt mit B… Tadaaa! Da ist deine Tangente! 🎉
Die "Ich-hab-keinen-Mittelpunkt"-Methode (Die Panik-Vermiedungs-Strategie)
Was, wenn du den Mittelpunkt *nicht* kennst? Keine Sorge, wir haben auch dafür einen Plan! Diese Methode ist ein bisschen trickreicher, aber hey, wir lieben Herausforderungen, oder? 😉
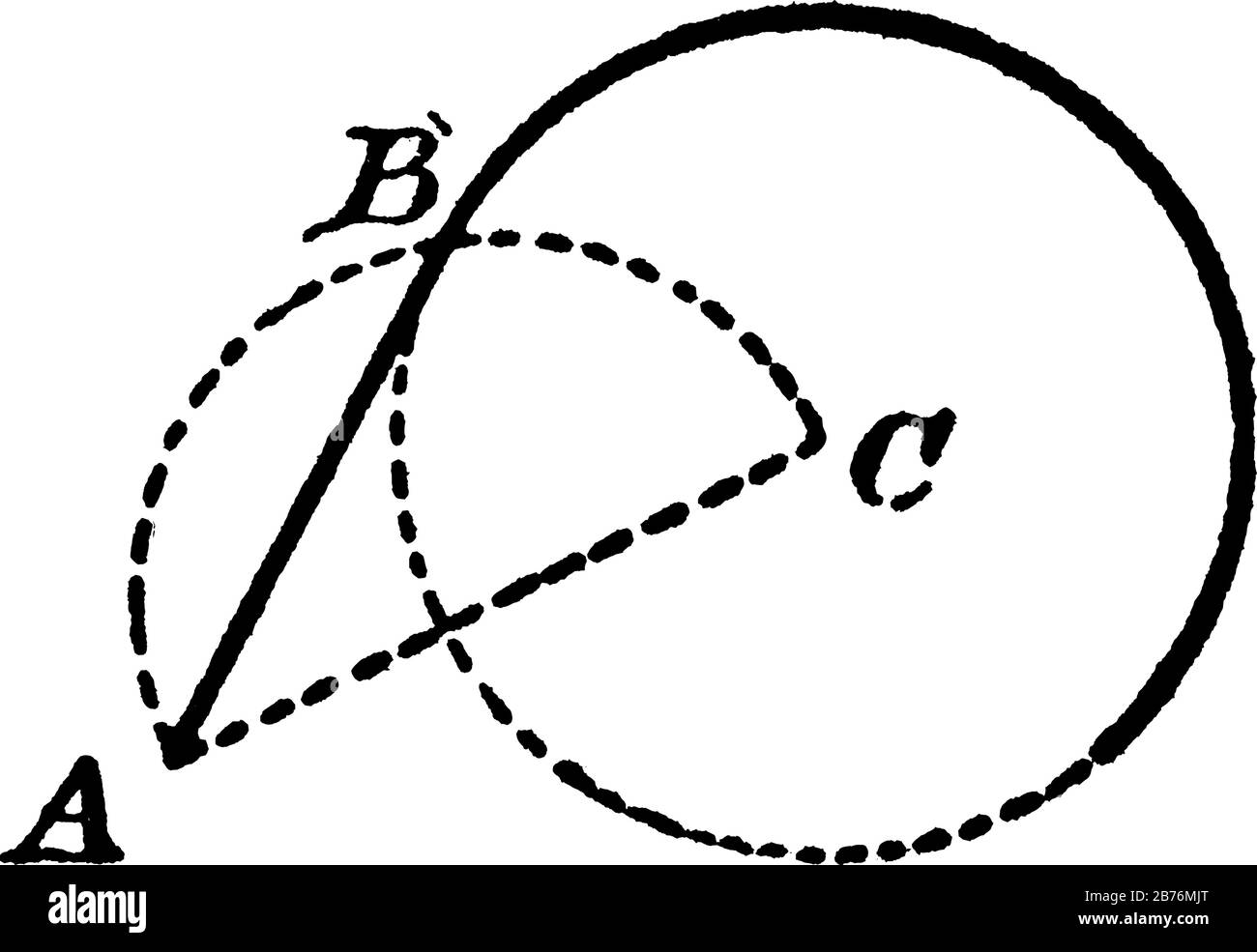
Wähle einen Punkt B auf dem Kreis, an dem die Tangente berühren soll. Dann wähle einen zweiten Punkt A auf dem Kreis. Zeichne die Sehne AB.
Jetzt kommt der Clou: Zeichne einen Winkel, der gleich dem Winkel im Kreissegment gegenüber der Sehne AB ist. Äh… was? Okay, einfacher gesagt: Stell dir vor, du verbindest A und B mit einem *dritten* Punkt C auf dem Kreis, der *nicht* zwischen A und B liegt. Der Winkel bei C ist der Winkel, den du "kopieren" musst.
Wie "kopiert" man einen Winkel? Wieder Zirkel-Zeit! Zeichne einen Bogen um den Winkel C. Dann übertrage diesen Bogen auf den Punkt B. Zeichne nun einen Bogen mit dem Radius, der dem Abstand der Schnittpunkte des ersten Bogens mit den Schenkeln des Winkels C entspricht, vom Schnittpunkt des zweiten Bogens mit der Sehne AB aus. Verbinde den Schnittpunkt der beiden Bögen mit B. Fertig! Das ist deine Tangente! Puh! 😅
Profi-Tipps und Tricks (Weil wir's können!)
Präzision ist Trumpf! Je genauer du zeichnest, desto besser wird das Ergebnis. Also, keine zittrigen Hände! 😉
Übung macht den Meister! Je öfter du diese Konstruktionen übst, desto leichter werden sie dir fallen. Und desto mehr kannst du damit angeben! 😎
Keine Angst vor Fehlern! Fehler sind menschlich und helfen dir, zu lernen. Also, nicht entmutigen lassen, wenn es nicht gleich klappt. Einfach nochmal versuchen!
So, jetzt bist du ein echter Tangenten-Konstruktions-Profi! Siehst du? Mathematik kann richtig Spaß machen! Du hast eine neue Fähigkeit gelernt, die nicht nur in der Schule nützlich ist, sondern auch zeigt, dass du Herausforderungen meistern kannst. Und das ist doch ein super Gefühl, oder? 😊 Geh raus, zeichne Tangenten und hab Spaß dabei! Du bist ein Mathe-Star! ✨