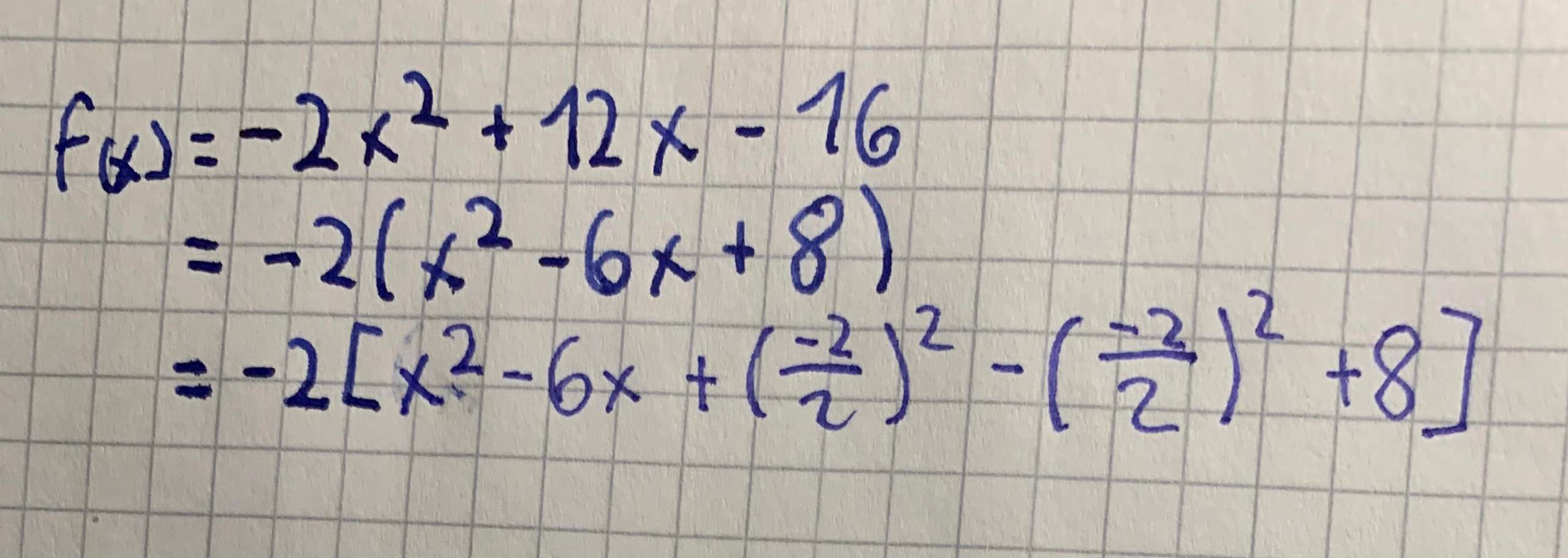Quadratische Funktionen – klingt erstmal nach trockenem Matheunterricht, aber glaub mir, da steckt mehr dahinter als man denkt! Stell dir vor, du bist ein Architekt, der eine perfekte Brücke entwerfen will, oder ein Basketballspieler, der den idealen Wurf sucht. Beides hat mit der Flugbahn eines Balls oder der Form einer Brücke zu tun, und die lässt sich oft mit einer quadratischen Funktion beschreiben. Klingt plötzlich spannender, oder?
Warum sind quadratische Funktionen so nützlich? Weil sie Parabeln beschreiben! Parabeln sind diese wunderschönen, sanft geschwungenen Kurven, die überall in der Natur und in der Technik vorkommen. Sie helfen uns, Bewegungen zu verstehen, Strukturen zu bauen und sogar die Zukunft vorherzusagen (zumindest in mathematischen Modellen!). Und um diese Parabeln zu beschreiben, benutzen wir quadratische Funktionen.
Es gibt verschiedene Arten, eine quadratische Funktion aufzuschreiben. Die zwei wichtigsten sind die Normalform und die Scheitelpunktform. Stell sie dir wie zwei verschiedene Sprachen vor, die aber beide dasselbe beschreiben. Die Normalform ist sozusagen die Standardsprache, die jeder kennt.
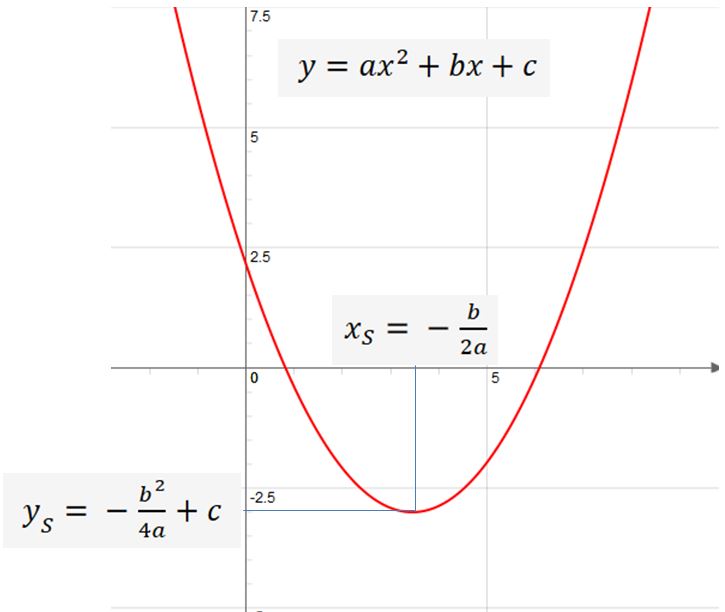
Die Normalform sieht so aus: f(x) = ax² + bx + c. Das "a", "b" und "c" sind Zahlen, die bestimmen, wie die Parabel aussieht. "a" bestimmt, ob die Parabel nach oben oder unten geöffnet ist (und wie breit oder schmal sie ist), "b" und "c" verschieben die Parabel im Koordinatensystem. Mit der Normalform kann man leicht den y-Achsenabschnitt ablesen (das ist nämlich einfach "c") und mithilfe der Mitternachtsformel oder der quadratischen Ergänzung die Nullstellen berechnen.
Die Scheitelpunktform ist etwas spezieller, aber super hilfreich, wenn du direkt den Scheitelpunkt der Parabel finden willst. Der Scheitelpunkt ist der höchste oder tiefste Punkt der Parabel – also der Punkt, an dem sie ihre Richtung ändert. Die Scheitelpunktform sieht so aus: f(x) = a(x - d)² + e. Hier ist "(d | e)" direkt der Scheitelpunkt! "a" hat dieselbe Bedeutung wie in der Normalform.
Der Vorteil der Scheitelpunktform ist also, dass du den Scheitelpunkt direkt ablesen kannst, ohne rechnen zu müssen. Das ist besonders praktisch, wenn du wissen willst, wo die Parabel ihren höchsten oder tiefsten Wert erreicht. Wenn du beispielsweise die optimale Flugbahn eines Balls berechnen willst, ist der Scheitelpunkt der höchste Punkt des Fluges.
Wie kommt man von der Normalform zur Scheitelpunktform? Ganz einfach: durch die quadratische Ergänzung! Das ist eine kleine algebraische Umformung, die etwas Übung erfordert, aber letztendlich nicht schwer ist. Es gibt auch Online-Rechner, die das für dich erledigen, wenn du es eilig hast.
Zusammenfassend lässt sich sagen: Die Normalform ist gut, um Nullstellen und den y-Achsenabschnitt zu finden, während die Scheitelpunktform perfekt ist, um den Scheitelpunkt direkt abzulesen. Beide Formen beschreiben dieselbe Parabel, nur aus unterschiedlichen Perspektiven. Also, keine Angst vor quadratischen Funktionen! Sie sind nützlicher (und unterhaltsamer) als du denkst!