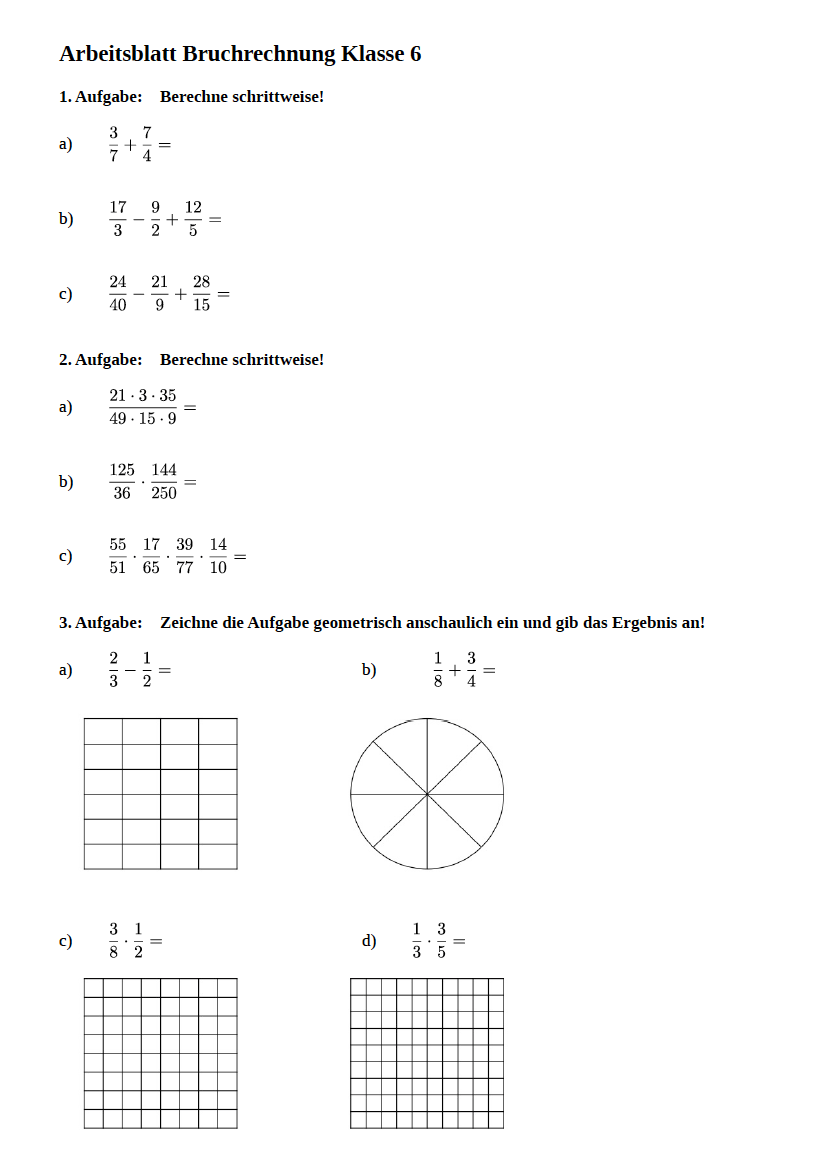Brüche vergleichen – das klingt erstmal nach trockener Mathematik, aber hey, eigentlich ist es wie ein kleines Spiel! Wer hat das größere Stück Pizza? Welches Rezept ergibt mehr Kuchen? Brüche vergleichen hilft uns, solche Fragen im Alltag zu beantworten. Und mit ein bisschen Übung wird es richtig easy!
Warum ist das Ganze nützlich? Für Anfänger ist das Vergleichen von Brüchen ein wichtiger Schritt, um das Konzept von Brüchen überhaupt zu verstehen. Man lernt, dass ein Bruch nicht einfach nur zwei Zahlen übereinander sind, sondern einen Teil eines Ganzen darstellen. Für Familien kann das Vergleichen von Brüchen beim Kochen und Backen helfen. Brauchen wir mehr Mehl, wenn wir ein Rezept verdoppeln? Und für Hobbyköche, die gerne mit Rezepten experimentieren, ist es unerlässlich, um Zutatenmengen anzupassen und das beste Ergebnis zu erzielen.
Stell dir vor, du hast zwei Pizzen. Die eine ist in 8 Stücke geteilt, und du nimmst 3 davon (3/8). Die andere ist in 4 Stücke geteilt, und du nimmst 1 davon (1/4). Welche Pizza hast du mehr? Um das herauszufinden, musst du die Brüche vergleichen. Es gibt verschiedene Wege, das zu tun. Eine Möglichkeit ist, die Brüche auf einen gemeinsamen Nenner zu bringen. In diesem Fall könnten wir 1/4 in 2/8 umwandeln. Jetzt ist es einfach: 3/8 ist größer als 2/8, also hast du von der ersten Pizza mehr gegessen. Eine andere Methode ist das Kreuzprodukt: 3/8 und 1/4, wir multiplizieren 3 mit 4 (12) und 8 mit 1 (8). Da 12 größer als 8 ist, ist 3/8 größer als 1/4.
Besonders beliebt bei Schülern der 6. Klasse sind Übungen im PDF-Format. Warum? Weil sie oft eine bunte Mischung aus Aufgaben bieten – von einfachen Vergleichen mit gleichen Nennern bis hin zu kniffligeren Aufgaben, bei denen man erst einen gemeinsamen Nenner finden muss. Außerdem sind sie praktisch, weil man sie ausdrucken und überall mit hinnehmen kann. Man findet viele kostenlose PDF-Dateien online, die speziell für diese Altersgruppe entwickelt wurden. Such einfach nach "Brüche vergleichen Übungen Klasse 6 PDF".
Praktische Tipps für den Start: Beginne mit einfachen Aufgaben, bei denen die Nenner gleich sind. Dann steigere dich langsam zu Aufgaben, bei denen du erst einen gemeinsamen Nenner finden musst. Nutze Visualisierungen! Male Kreise und teile sie in Stücke, um Brüche darzustellen. Das hilft, das Konzept besser zu verstehen. Und vergiss nicht: Übung macht den Meister! Je mehr du übst, desto leichter wird es dir fallen, Brüche zu vergleichen.
Also, keine Angst vor Brüchen! Mit ein bisschen Übung und den richtigen Hilfsmitteln wird das Vergleichen von Brüchen zum Kinderspiel. Und wer weiß, vielleicht entdeckst du sogar, dass Mathe richtig Spaß machen kann! Denn am Ende geht es darum, die Welt um uns herum besser zu verstehen, und Brüche sind ein wichtiger Teil davon. Und das ist doch etwas, worauf man stolz sein kann!